[알고리즘 / C++] DFS(깊이 우선 탐색) 알고리즘 개념 및 스택과 재귀를 활용한 구현
DFS(깊이 우선 탐색) 역시 앞서 포스팅했던 BFS 알고리즘과 마찬가지로 길찾기 알고리즘을 구현할 때 유용한 그래프 탐색 알고리즘입니다. Brute Force(완전탐색) 형태로 모든 경우의 수를 다 시도하여 답을 찾는 방법으로, 이름과 같이 깊이(Depth)를 끊임없이 추적하며 전체 정점을 탐색합니다.
앞서 인접행렬과 BFS탐색 알고리즘에서 보였던 아래와 같은 그래프와 인접행렬을 예로 들어보겠습니다.
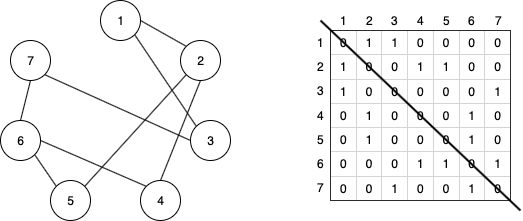
1부터 탐색을 시작한다고 가정할 때, BFS가 2와 3을 큐에 담는 것과 달리, DFS는 오직 가장 근접한 값인 2만 스택에 담습니다. 그리고 두번째 뎁스인 2에서 다음 탐색을 이어갈 정점을 찾습니다. 1,4,5가 2와 연결되어있지만, 1은 이미 탐색을 마쳤고, 5보다 빠른 4가 있기 때문에 다음 뎁스로 4를 탐색합니다. 이런식으로 끊임없이 뎁스를 찾아가며 탐색을 이어갑니다.
1->2->4->6->5까지 이어간 이후, 5에서 정점을 탐색할 때 다음 뎁스로 이어갈 경로가 없습니다. 2와 6이 5와 연결되어 있으나, 둘 다 이미 탐색을 마쳤기 때문에 갈 길이 없습니다. 이때는 스택에서 pop합니다. pop 한 후 이전 정점이었던 6에서 탐색을 이어갑니다. 이후 6->7->3 순으로 탐색을 마치고 전체 스택에 있는 값을 차례대로 비워가며 탐색을 마칩니다.
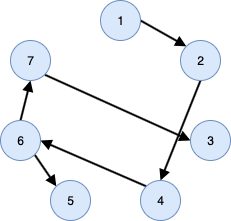
글로 설명한 DFS 예시를 그림으로 표현하면 다음과 같습니다.

본 예시에서 pop은 단 한번(5에서) 발생합니다. 하지만 앞서 설명드린 바와 같이, pop은 더이상 진행할 경로(뎁스)가 없지만 아직 탐색해야 할 정점이 남은 경우, pop을 진행한다는 점을 기억해야 합니다. 또한 DFS에서는 큐가 아닌 스택을 사용해야 한다는 점을 명심해야 합니다. 최종 탐색 경로를 정리하면 다음과같습니다.
앞서 DFS 그래프 탐색 알고리즘은 스택을 사용하여 구현할 수 있다고 했습니다. 대부분은 앞서 구현한 BFS와 비슷합니다. 하지만 큐가 아닌 스택을 썼다는 점과 exist_subdepth 변수를 통해 다음 뎁스가 존재하는지를 검사하는 부분을 추가하였습니다. (참고: 인접행렬과 BFS탐색 알고리즘)
아래 코드를 참고할 때 유념해야 할 사항이 몇 가지 있습니다.
- 간선(edge) 정보: 인접행렬 정보를 이중 벡터로 구성.
- 방문한 노드 리스트(vertices): 이미 방문한 적이 있는 노드의 경우, 어딘가에 기록해 둬야 합니다. 앞서 BFS 구현과 마찬가지로 vertices에 정점 방문에 대한 기록을 저장합니다.
- 방문한 노드 표시(Visited): 임시로 방문했음을 표시.
- 방문하지 않은 노드 표시(Unvisited): 아직 방문하지 않은 값. 특히 간선으로 연결되어 있는 경우에만 유효.
- stack: 방문한 정점을 순서대로 push 한다. 다음 이동할 정점이 없는 경우에는 pop한다.
- DFS(): DFS 탐색을 위한 함수. 주의할 점은 첫 정점은 반드시 일단 stack에 push하고 시작한다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#define VISITED 1
#define UNVISITED 0
#define CONNECTED 1
using namespace std;
// 행과 열 사이즈가 동일해야 함.
vector<vector<int> > edge =
{
{0, 1, 1, 0, 0, 0, 0},
{1, 0, 0, 1, 1, 0, 0},
{1, 0, 0, 0, 0, 0, 1},
{0, 1, 0, 0, 0, 1, 0},
{0, 1, 0, 0, 0, 1, 0},
{0, 0, 0, 1, 1, 0, 1},
{0, 0, 1, 0, 0, 1, 0}
};
vector<int> vertices;
void DFS(int vertex_idx)
{
vertices.at(vertex_idx) = VISITED;
stack<int> s;
s.push(vertex_idx);
cout << vertex_idx+1 << " ";
while (!s.empty())
{
int target_vertex = s.top();
bool exist_subdepth = false;
for (int i = 0; i < edge.size(); i++)
{
if (edge.at(i).at(target_vertex) == CONNECTED && vertices.at(i) == UNVISITED)
{
cout << i+1<<" ";
s.push(i);
vertices.at(i) = VISITED;
exist_subdepth = true;
break;
}
}
if(!exist_subdepth)
s.pop();
}
}
int main()
{
vertices.assign(edge.size(),UNVISITED);
for (int i = 0; i < edge.size(); i++)
{
if (vertices.at(i) == UNVISITED)
{
DFS(i);
}
}
cout << endl;
return 0;
}
위의 코드에서 보는 것과 같이 BFS 구현과의 차이는 큐가 아닌 스택을 사용했다는 점과 다음 뎁스가 존재하는지 확인하여 pop을 한다는 점입니다. 그 외에는 대부분 BFS와 비슷합니다.
결과:
1 2 4 6 5 7 3
DFS알고리즘은 재귀함수를 활용하여 구현할 수 있습니다. 이때는 스택대신 재귀를 사용하여 백트래킹 합니다.
- DFS(): 함수 자체가 재귀적으로 동작합니다. 본 함수 자체가 뎁스를 의미하기도 합니다.
#include <iostream>
#include <vector>
#include <algorithm>
#define VISITED 1
#define UNVISITED 0
#define CONNECTED 1
using namespace std;
// 행과 열 사이즈가 동일해야 함.
vector<vector<int> > edge =
{
{0, 1, 1, 0, 0, 0, 0},
{1, 0, 0, 1, 1, 0, 0},
{1, 0, 0, 0, 0, 0, 1},
{0, 1, 0, 0, 0, 1, 0},
{0, 1, 0, 0, 0, 1, 0},
{0, 0, 0, 1, 1, 0, 1},
{0, 0, 1, 0, 0, 1, 0}
};
vector<int> vertices;
void DFS(int vertex_idx)
{
vertices.at(vertex_idx) = VISITED;
for (int i = 0; i < edge.size(); i++)
{
if (edge.at(vertex_idx).at(i) == CONNECTED && vertices.at(i) == UNVISITED)
{
cout << i+1<<" ";
DFS(i);
}
}
}
int main()
{
vertices.assign(edge.size(),UNVISITED);
for (int i = 0; i < edge.size(); i++)
{
if (vertices.at(i) == UNVISITED)
{
cout << i+1 << " ";
DFS(i);
}
}
cout << endl;
return 0;
}
결과:
1 2 4 6 5 7 3'Development > Algorithm' 카테고리의 다른 글
| [Algorithm / C++] 인접행렬과 BFS (너비 우선 탐색) 알고리즘 및 구현 (0) | 2019.12.26 |
|---|---|
| [Algorithm / C++] String을 파싱하는 3가지 방법 (0) | 2019.12.26 |
| [Algorithm / C++] BackTracking 기법을 활용한 순열(Permutation)과 조합(Combination) 구현 (0) | 2019.12.25 |






